ESPERANZA MATEMATICA

Con frecunecia es conveniente calcular el promedio de los resultados del proceso o experimento ponderado por la probabilidad de que suceda cada una de los resultados posibles. A este promedio se le conoce como EM.

COMENTARIO: Esto es el resultado para experimentar todas los resultados de las probabilidades que puedan suceder en un experiento

CLASIFICACION DE LA PROBABILIDAD

LA PROBABILIDAD CLASICA: Supone que todos lo9s eventos tienen la misma probabilidad de ocurrir esta es la relaciòn de nùmeros de eventos señalados respecto al total de eventos posibles.

Ejemplo: Si en una caja hay 50 manzanas y 200 naranjas la probabilidad de que al tomar una fruta esta sea manzana.

COMENTARIO: todos los problemas tienden a dar la misma respuesta utilizando la misma formula para obtener un numero de actividades posibles.

LA PROBABILIDAD OBJETIVA: Define a la probabilidad como la relacion entre el numero de eventos favorables obtenidos respecto al total de intentos.

Ejemplo: si en una caja que contiene manzanas y naranjas se han tomado 80 frutas y de estas 15 han sido manzanas se deduce que al sacar una fruta de la caja la probabilidad va a ser de que sea manzanas
P(M)= 15/80= 0.99=90%

COMENTARIO: ESTA SE VA A DAR cuando se tome y se enlace las respuestas pra dar el resultado exacto con el total de insistencias del resultado.

ARBOL DE PROBABILIDADES: UN ARBOL DE probabilidad es una gràfica que presenta los resultados posibles ( opciones de un evento), asi como la probabilidad de cada uno de ellos.

Ejemplo: En una fabrica de alfileres logra una produccion de alfileres defectuosos.

COMENTARIO: eSTE estudia las posibles respuestas de una grafica para determinar una probabilidad y asi darla a conocer.

PROBABILIDAD

Calcula la continuidad de las respuestas que son resultantes de la realizaciòn de algùn experimento o prueba. La probabilidad (relacion entre el nùmero de resultados de un respecto al total de resultados posibles) puede ser objetiva o subjetiva. La primera es resultados de calculos mientras que la subjetiva solo emiten o refleja la persepcion de quien la ejecuta.

Ejemplo: tiramos un dado al aire y queremos saber cùal es la probabilidad de que salga un 2, o que salga un nùmero par, o que salga un nùmero menor que 4.


COMENTARIO: LA PROBABILIDAD son las posibles respuestas que pueda tener un evento o actividad y se calcula por medio de un experimento o prueba

EXPERIMENTOS DE LA PROBABILIDAD PUEDEN SER:

ALEATORIO: Esto es cuando se dan diferentes respuestas, con el mismo procedimento para realizar el experimento, en cùal pueden ser respondidas con varias alternativas solo existe un problema al a ver tantos resultados y es no saber cual de todos mostrar.

Ejemplo:lanzamos una moneda al aire el resultad puede ser cara o cruz, pero no sabemos de antemano cùal de ellos va a salir.

COMENTARIO: Esto se da cuando tenemos muchas o demasiadas respuestas de un experimento pero todas son diferetes es en teoria bueno pero ñla unica desventaja es que no se sabe cual de todos podemos dar a conocer.

NO ALEATORIOS: A estos experimentos no se le puede someter las reglas quse tiene la proababilidad.

Ejemplo:En lugar de tirar la moneda al aire, derectamente seleccionamos la cara. Aqui no podemos hablar de probabilidades, sino que hasido un resultado determinado por uno mismo.

COMENTARIO: Este tipo de experimentyos no pueden ser calculados con las formulas ya que solo podemos tomar el resultado que queremos sin necesidad de hacer calculos matematicos para lograr lo que queremos.

Para realizar algun experimento tomando como base los calculos probabilisticos en la cùal se tiende a definir una serie de concepto:

SUCESO ELEMENTAL: Esta insinua a todas las respuestas sin excluir alguna de las alternativas que se puedan dar:

Ejemplo: Al lanzar una moneda al aire, los sucesos elementales son la cara y la cruz. Al alzar un dado, los sucesos elementales son el 1 el 3..., hasta el 6.

COMENTARIO: Este expone todas las respuestas que nos da el resultado de un experimento para que tengamos varias soluciones.

COMENTARIO SOBRE PERMUTACION Y COMBINACION:

PERMUTACION: Es cuando cambiamos de lugar.

COMBINAR: COMBINAR O COLOCAR SIN IMPORTAR EL LUGAR.

TEORIA DEL CONTEO

Algunos tópicos sobre Conjuntos.
La teoría de conjuntos es de mucha utilidad en el desarrollo de las probabilidades, y es por ello que se debe revisar los conocimientos sobre las operaciones de conjuntos como lo son: la unión, la intersección, el complemento de un conjunto, etc.
.- Consideraremos a W como el conjunto universal el cual posee todos los elementos posibles, así el conjunto A es un subconjunto de W si todos los elementos de A son elementos de W, y se denota:
A Ì W si para todo x ÎA, x Î W
.- Sean A y B dos conjuntos cuales quiera entonces:
la unión se define como: C = A È B = { x / xÎA o xÎB};
la intersección se define como: C = A Ç B = { x / xÎA y xÎB};
el complemento se define como: Ac = { x Î W / x Ï A },
El conjunto que no posee elementos se denomina conjunto vacío y se denota por Æ . (Notemos que A Ç Ac = Æ )
Diremos que A y B son disjuntos o mutuamente excluyente si: A Ç B = Æ.
Para resolver algunos problemas de probabilidades es necesario conocer el numero de elementos que posee cierto conjunto y el conjunto universal, denominado, en probabilidades, espacio muestral, es por ello que se debe saber como determinar el número de elementos de cualquier conjunto, tarea que puede ser algo complicado, sin embargo en algunos casos esto se puede realizar y por ello es que es importante el aprender a calcular este número.
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Técnicas de Conteo
Debes recordar la regla principal en las Técnicas de Conteo como lo es la ley de multiplicación:
Si se tienen n elementos de un tipo y m de otro, el número de parejas que se pueden formar tomando un elemento de cada tipo es
mxn.
Las permutaciones, las variaciones y las combinaciones, resultan de la regla de multiplicación.

COMENTARIO:

La teoria del conteo conteo es muy esencial para los calculos prebabilisticos ya que de una x cantidad pede salir una serie de resultados utilizando todos sus miembros e irlos desglosando para conyevar un determinado numero de conjuntos.

TENDENCIA CONSTANTE

La tendencia constatnte tiene unefecto queprovoca por esta componente, en general no mensurable, es de corta duracion e intensidad variable ( desde imperceptible hasta la mudanza en la propia direcciòn de las tendencias y ciclos) esta tiende a cambiar tento de variable como de tamaño y direccion.




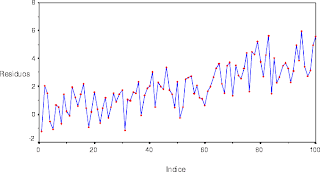
COMENTARIO:

La tendencia constante especialmente en fisica se denomina constante ya que es cuando su valor no tiende a cambiar en el tiempo, ya que posee un valor fijo, auque a veces no es determinado.

La tendencia constante se hace con valores que en el diagrama de dispercion se vean constantes, es decir, seguidos con sus bajas y subidas en la cual se guia con un linea horizontal de la cual le ayuda a guiarse eso si no varia o no cambia mucho en el transcurso del tiempo.






TENDENCIA DETERMINISTA

La tendencia determinista es un mètodo tradicional en la que se acostumbra a tomar las descomposiciones de una serie en tres componetes la Lìnea de tendencia, una componente estacional y la ultima una parte irregular, asi surge una formula matematica que permite calcular una recta que se hacerca mas a la curva de los datos.

COMENTARIO:

La tendencia determinista su linea tendencial siemprese calcula en una recta creciente la cùal se extiende de forma estacional y tiene la sima o punta del decenso de la tendecia en la cual posee una variable irregular, ya que su tendencia es determinista si conocemos sus valores pasados se puede determinar sin ERROR sus valores futuros con tendencias deterministas no hay ningun incombeniente sobre ella, en esto comprendi que la tendecia lineal que posee resta de la original es decir de datos anteriores para su ajuste.

La tendencia determinista posee variabilidad.

TENDENCIA EVOLUTIVA:

Las series evolutivas, a menudo , la tendencia de la tendencia no sigue una recta y evoluciona a lo largo del tiempo, un metodo general de estima la tendencia es de suponer que la tendencia es una funcion que evoluciona lentamente en el tiempo,y que se puede aproximar con una funcion sencilla en intervalos cortos del tiempo.,.,,

La tendencia evolutiva es una curva que va cambiando lentamente en una suposiciòn, los puntos de esa curva se calculan con la media movil.

COMENTARIO:

La tendencia evolutiva no es una linea recta ya que a la larga va cambiando y con eltiempopresenta una serie de intervalosque cambia lentamente, ya que la tendencia evolutiva es una curva en la en el transcurso del tiempo a decrecido minimamente pero su tendencia se forma ascendentemente, es si este tipo de tendencia no sigue una tendencia lineal sino que evoluciona a la larga y toma diferentes caracteristicas y formas de prediccion.

METODO DE DOS PROMEDIOS:

El modelo de las series de tiempo como lo son el metodo de dos promedios esto se representan acorto plazo que pronostica las ventas para el siguiente periodo.

Para ello, promedia los datos de unos cuantos periodos recientes y este promedio se convierte en el prònostico del pèriodo siguiente. Cuanto mayor sea la cantidad de periodos promediados, mayor es la capacidad de amortiguaciòn del ruido y menor es la respuesta de impulso del pronostico y viceversa.

COMENTARIO:

El metodo de dos promedios en esta comprendi que se divide la las datos para graficar en dos partes, se busca el promedio de cada parte y se ajusta una linea de tendencia quepasa por los promedio que deben ser marcados con algun simbolo que los logre identificar y asi trasar nuestra linea, ya que se encuentra en si entre dos datos las cuales se opera con los datos de "Y" y se divide por "Z" para encontrar las 2 medias para trasar una lìnea.

para realizar la grafica primero en el cuadro tomamos por ejemplo 5 datos en el cual tomamos el o la fila de en medio, luego a "X" se divide por "Y", y la segunda parte es de manera, repetida. Los resultados que salgan de estos dos son los promedios que tomamos para trasar nuestra tendencia.

SERIES NO ESTACIONARIAS

Es la que procede a estudiar las diferentes transformaciones y irregularidades de los datos, para calcular una posible funcion matematica.
Ya que su proceso y propiedades tienden a cambiar en el tiempo y se guia por medio de la media, esto lo utiliza para guiarse y asi poderce deferenciar de las series estacionarias, ya que estas en un periodo determinado se presente con espacios cronologicos.


COMENTARIO:
las series no estacionarias se guian por el numero de promedio de datos que posee para realizar la grafica ya que este le sirve para determinar su tendencia y asi poder diferenciarce de las series estacionarias ya que estas son las que se pueden representar por un histograma, las series no estacionarias poseen cambios en el transcurso del tiempo la cual grafica sus irregularidades y asi se denominan no estacionarias.



Variables
Una variable es un nombre asociado a un elemento de datos que está situado en posiciones contiguas de la memoria principal, y su valor puede cambiar durante la ejecución de un programa.
Toda variable pertenece a un tipo de dato concreto. En la declaración de una variable se debe indicar el tipo al que pertenece.
Variables introducción a las variables: qué son y cómo usarlas.
Descripción del alcance de las variables Análisis de cómo se aplica el alcance a las variables.
Temas avanzados sobre variables Información detallada sobre las variables.
Variables estáticas introducción a la utilización de variables estáticas para preservar valores.
Constantes Introducción a la utilización de constantes para representar valores.
Tipos de datos Análisis de los tipos de datos disponibles en Visual Basic.
Temas avanzados sobre el tipo de dato Variant Información detallada sobre el tipo de dato Variant.
Matrices Introducción a la utilización de matrices para grupos de valores.
Matrices dinámicas Análisis sobre la utilización de matrices dinámicas para trabajar con grupos de valores


COMENTARIO:
Las series variables son las que se mantienen en un posicion continua y estable lo cual le ayuda a graficarse con los datos y el numero de promedios y se traza un linea horizontal para determinar su tendencia y definir si cambia con el tiempo y asi detallar su posicion.

COMENTARIO:
Las series de tiempo son graficas deben ser observadas muy intensamente, las variables las podemos observar que no se puede ordenar de mayor a menor, ya que si esto se hace perderia valor la variable, posee un orden cronologico en el cual podemos observar la agudeza y la tendencia tiende a evolucion ar con el tiempo ya sea que poseea una larga duracion o no.
Las series temporales ayudan a explicar y a describir los procesos para la elavoracion grafica de los datos para realizar un representacion grafica.

SERIES ESTACIONARIAS

Un concepto importante que encontramos en este ámbito, es el de procesos estacionarios. Si examinamos por ejemplo la temperatura para un determinado mes a lo largo de los años en una determinada zona geográfica, y se está produciendo un cambio climático, aunque haya fluctuaciones, habrá una tendencia creciente. De una manera informal, diremos que una serie es estacionaria cuando se encuentra en equilibrio estadístico, en el sentido de que sus propiedades no varían a lo largo del tiempo, y por lo tanto no pueden existir tendencias.


COMENTARIO:
Las series estacionarias esta muestra una tendencia que posee cambios que se observan con el tiempo ya que como su nombre lo dice se mantiene estable ya que si cambia, lo hace en el transcurso del tiempo, pero sigue una sevcuencia deuna linea vertical recta en la que posa sus cambios y desde allì se puede observar sus cambios, pero de forma no muy constante

SERIES DE TIEMPO

Series de Tiempo

Una serie temporal o cronologica es un conjunto e observaciones de una variable, ordenadas segu transcurre el tiempo.

En una serie de tiempo las observaciones no se deben ordenar de mayor a menor debidoa que se perderia el grueso de la informacion debido a que nos intersea detectar como se mueve la variable en el tiempo es muy importante respetar la secuencia temporal de las observaciones.

e presentan Series de Tiempo para puntos de la región seleccionada. La gran parte de las opciones corresponden a lo mencionado para los cortes verticales.
Debido a que se trata de representaciones puntuales en el espacio no existe la opción de marcar la opción latitud o longitud sino hay que indicar un valor para ambos parámetros definiendo así un punto en el área de la región seleccionada. Igualmente existe la opción de seleccionar una zona climática como explicado anteriormente.

REGRECION Y CORRELACION

REGRESION:

La palabra se emplea para denotar el proceso de estimar el valor de una de las variables en funcion de la otra, cuyo valor se considera dado. Galton fue el primero en utilizar el termino, en un estudio que hizo para relacionar las estaturas de padres e hijos, indicando un regreso hacia los atributos del padre.

Cuando se calcula el valor de X e funcion de Y, se habla de una regresion de "1 en 2" y se estará calculando la primera variable en funcion de la segunda . La regresion de "2 en 1" será cuando calculemos el valor para Y, si conocemos el valor de X.

La ecuación Y=a +b X, que describe la relacion entre las variables X y Y, se llama ecuacion de REGRESIÓN y su gráfica, RECTA DE REGRESIÓN.

COMENTARIO:

La regresion es una estimacion entre dos variables las cuales son CAUSA y EFECTO, de estas variables se parte para poder determinar hacia donde se va a dirigir la linea que se representa en un diagrama de DISPERSION, las lineas en este diagrama pueden ser ASCENDENTES: si es mayor que cero, o sea pendiente positiva, DESCENDENTE: si es menor de cero, o sea pendiente negativa o UNA LINEA PARALELA A UNO DE LOS EJES: si es igual a cero, las cuales se dibujan en el diagrama de dispersion con una linea imaginaria continua.

CARACTERISTICAS DEL DIAGRAMA DE CAJAS

Suministra informacion sobre la mediana, el cuartil Q1, Q2, Q3 sobre la existencia de atipicos y la simetria de la distribucion.

El diagrama de cajas se presenta solo un eje, se representan cinco valores: los valores minimos y maximo, la primera y tercer cuartil y la mediana que proporcionan informacion completa visualizada sobre como se distribuyen los datos. Simetria o no, los diagramas de cajs proporcionan una idea intuitiva de la simetria de la distribucion de los datos: si la media no esta en el centro del rectangulo eso significa que la distribucion no es simetrica, conociendo ademas a que lado se escoja.

¿COMENTARIO?

Las caracteristicas que màs se destacan son los bigotes y que se colocan a los lados de la caja o bateriay la grafica puede colocarce de forma horizontal o vertical y destacar asi los datos prestablecidos por la frecuencia y tiene forma de bateria y se puede representar por cuatiles y su simetria debe ser exacto sugun sus datos.

Los datos maximos y minimos influyen mucho en la colocacion de los bigotes para la realizacion de la grafica.

RELACION ENTRE EL DIAGRAMA DE CAJS Y LA CURVA

El diagrama de cajas describe al mismo tiempo varias partes importantes de un conjunto de datos tales como el centro, la dispercion, el alejamiento de la simetrìa, y la identificacion de valores que se alejan de una manera poco usual del resto de los datos.

El area bajo la curva es la que posee 100% de todos los casos de una distribucion dada, ya que el àrea bajo la curva es asintotica, porque las colas de la curva no pueden tocar la linea base y su altura naxima se encuentra el area o sea la media ,ya que en este caso es el promedio de la distribucion de datos tabulados.

¿COMENTARIO?

La relacion existente entre estos metodos de dispercion es en que ambas toman como medio o mitad, la media ya que es el porcentje de la distribucion de una seri de numero. Estudia que tan alejados estan los datos, y representan los datos que caen en la media.

EVALUACION POR PORTAFOLIO

“Portafolio" se conceptualizará como un conjunto de evidencias respecto al conocimiento y las habilidades que van a adquirir los estudiantes a través de la práctica. Este puede ser utilizado para diversos propósitos, el modelo está basado en la aplicación de principios constructivistas acerca del aprendizaje, la enseñanza, y las formas de recolección de información.

Propuesta de trabajo y evaluación del modelo constructivista “portafolio", usado como metodología de enseñanza-aprendizaje en dos de los cursos que presentan mayor dificultad para los estudiantes de la Escuela de Bibliotecología, Documentación e Información: Almacenamiento y Recuperación de Información 1 y Metodología de la Investigación. Esta metodología se implementó como una respuesta a la necesidad de desarrollar un proceso que permita a los estudiantes asimilar los contenidos de los cursos de acuerdo con sus propias experiencias y concepciones.
La metodología fue evaluada para determinar su efectividad en el proceso enseñanza aprendizaje, esta evaluación se realizó en el transcurso del semestre y al final del mismo, a través de un cuestionario, un taller de evaluación y la revisión del portafolio elaborado por los estudiantes.

¿COMENTARIO?

El portafolio es un metodo de trabajo muy amplio ya que busca que los alumnos aprendan a buscar informacion en distintas fuentes, ayuda a los alumnos a plantearce difiniciones propias del tema que se les halla sido propuesto por el catedratico.

El portafolio es una especie de evidencia que le deja a los estudiantes para que aprendan a desempeñarce por si solos una serie de ejercicios que el catedratico les halla enseñado para que ellos asi puedan guiarce y terminar los ejercicios que el profesor les halla enseñado.

AREA BAJO LA CURVA

Es el area que esta bajo la curva y la linea base y que tiene el 100% de todos los casos en una distribucion normal dada al estudiar una proporcion constante del area total bajo la curva normal estara entre la media en cualquier distancia dada en x.

¿COMENTARIO?

El area bajo la curva es utilizado para calcular el area y asi poder ocupar el porcentaje que se encuentra en la curva normal en la cual es llamada curva de campana o curva de error para lograr diseñar los datos, las frecuencias de una distribucion dentro de la campana se debe tomar como centro o mitad la media y asi saber donde se deben colocar los datos ya que en la media se encuentra la altura maxima y se le denomina unimodal por que solo tiene un punto maximo de frecuencia.

PORCENTAJE DEL AREA BAJO LA CURVA

¿COMENTARIO?

Nos sirve para saber los porcentaje s que son el resultado de la operacion (Z) que para aplicar esto necesitamos los datos de la desviacion estandar, la media y el numero de datos de la distribucion.

Cuando nosotros obtenemos el resultado de nuestra operacion debemos emplear el uso de la tabla de distribucion del area y multiplicar la cantidad de nuestra operacion por 100 para obtener el porcentaje y asi poder ubicarlo en nuestra curva y poder denominar si es positiva, negativa o neutral o igual a 0.

VALORES ESTANDARIZADOS (Z)

El puntaje z o estandar que indica la dirreccion y el grado que cualquier puntaje crudo se desvia de la media en una distribucion en una escala de unidades.

¿COMENTARIO?

El valor Z nosotros para aplicarlo debemos de operar en su formula z = a la media menos numero de datos y debido la desviacion estandar y el resultado lo debemos de colocar dependiendo de la denominacion que nos de si es positiva o negativa.

DIAGRAMA DE CAJAS

Los diagramas de cajas y bigotes (boxplot o box and whiskers) son una presentacion visual que escribe varias fases importantes al mismo tiempo como la simetria y la dispersion su presentacion es sobre un rectangulo que esta alineado vertical e horizontalmente.

¿COMENTARIO?

El boxplot o el diagrama de bigotes y cajas en esta grafica se representa graficamente como una bateria ya sea vertical e horizontalmente. Se estudia un conjunto de datos que se encuentra dispersos tomando los datos de los extremos de la grafica y asi identificarlos y ver como estan alejados unos datos con otros de esta manera podremos obtener la informacion necesaria para realizar nuestra grafica.

ESTADISTICA

¿Qué es estadística?
La estadística es una colección de métodos para planificar y realizar experimentos, obtener datos y luego analizar, interpretar, y formular una conclusión basada en esos datos. Es la ciencia encargada de recopilar, organizar, analizar e interpretar información numérica o cualitativa, de manera que pueda llevar a conclusiones válidas.

¿COMENTARIO?


Es una forma que sirve para poder obtener datos por medio del analisis para poder organizar y dar significado una cierta cantidad de informacion es decir datos, para llegar a conclusiciones valederes.







¿QUE ES UNA VARIABLE?


Se refiere a una caracteristica que se mide en el estudio. en terminos estaditicos rigurosos, una variable es la representante de esas mediciones en el analisis. los datos medidos en una escala continuan u ordinal se expresan por medio de una variable. Es al que cambia o varia con diferentes cualidades. las variables pueden ser:



VARIABLES CUALITATIVAS:
Son las vaiables que expresan distintas cualidades, caracteristicas o modalidad. Cada modalidad que se presenta se denomica atributo o categoria y la medicion consiste en una clsificacion de dichos atributos. Las variables cualitativas pueden ser ordinales y nominales.



1. VARIABLE CUALITATIVA ORDINAL: La variable puede tomar distintos valores ordenados siguiendo una escala establecida, aunque non es necesaria que el intervalo entre mediciones sea uniforme.



2. VARIABLE CUALITATIVA NOMINAL: En esta variable los valores no pueden ser sometidos a un criterio de orden.



VARIABLES CUANTITATIVA:
Son las variables que se expresan mediante cantidades numericas cuantitativas ademasn pueden ser discretas y continuas.


1. VARIABLE DISCRETA: Es la variable que presenta separaciones o interrupciones en la escala de valores que puede tomar.


2. VARIABLE CONTINUA: Es la variables que puede adquirir cualquier valor dentro de un intervalo especifico de valores.



¿COMENTARIO?
En este tema es basico para la estadistica por que en esto se basan varias operaciones y problemas numericos.Las variables son representaciones de mediciones o puede cambiar por medio de variables ordinales u continuas, adoptando diferentes valores en cada uno de los casos de un estudio.



Las variables cualitativas son las que se expresan por mediante caracteristicas y modalidades o cualidades. como lo son las variables ordinales y nominal.





Las variables ordinales son las que llevan una escala como: abecedario, leve, calendario.


Las variables nominales son las que no puede ser ordenadas como: los colores , las huellas digitales.





Las variables cuantitativas son las que se expresan medinate cantidades nùmericas.Como lo son las variables discretas y continuas.



Las variables discretas son las que no se pueden contar como un numero entero, el numero de hijos.


Las variables continuas son las que siguen una regla numerica como 1 dividido en 1000.



MEDIDAS DE TENDENCIA CENTRAL
Al analizar la informacionestadistica observamos un significativo comportamiento de los datos en cuanto a la frecuncia con que se presentan los valores y que algunos de estos valores son mas frecuentes que otros. Por lo que la mayor densidad de las frecuencias esta en la parte central de las graficas y ahi se deriva el nombre de MEDIDAS DE TENDENCIA CENTRAL o PROMEDIOS CENTRALES. La media aritmetica se representa por MEDIA, MODA, MEDIANA.



LA MEDIA o media aritmética de “n” datos numéricos es el cuociente entre la suma total de estos, dividida por “n”. La formula se representa asi:









LA MODA de una muestra de datos es aquel que presenta la mayor frecuencia.









LA MEDIANA es un conjunto de datos numéricos ordenados en forma creciente o decreciente, la mediana es el dato que se encuentra en el centro de la ordenación














VARIANZA:
Si elevamos al cuadrado las desviaciones logramos que todas las desviaciones den resultado positivos, luego si sumamos los cuadrados de las desviaciones y las dividimos dentro del nùmero de datos obtendremos la varianza que sirve de base para calcular la desviacion estandart.

DESVIACION TIPICA O ESTANDAR:
Es la media cuadratica de las desviaciones con respecto al promedio aritmetico es la raiz cuadratica de la media aritmetica de los cuadrados de las desviaciones de los datos de las desviaciones de los datos de la serie respecto a su media aritmetica.












DESVIACION MEDIA:
Es la media aritmetica de las desviaciones respecto a la media tomadas en valor absoluto, o sea es la suma de las desviaciones absolutas de todas las observaciones desde su media aritmetica, la cual es dividir entre numeros de observaciones.

MEDIA ARMONICA:
La media armónica , representada por H, de una cantidad finita de números es igual al recíproco, o inverso, de la media aritmética de los recíprocos de dichos números
Así, dados los números a1,a2, ... , an, la media armónica será igual a:

La media armónica resulta poco influida por la existencia de determinados valores mucho más grandes que el conjunto de los otros, siendo en cambio sensible a valores mucho más pequeños que el conjunto.
La media armónica no está definida en el caso de la existencia en el conjunto de valores nulos.

MEDIA CUADRATICA:

La media cuadrática es igual a la raíz cuadrada de la suma de los cuadrados de los valores dividida entre el número de datos:
A veces la variable toma valores positivos y negativos, como ocurre, por ejemplo, en los errores de medida. En tal caso se puede estar interesado en obtener un promedio que no recoja los efectos del signo. Este problema se resuelve, mediante la denominada media cuadrática. Consiste en elevar al cuadrado todas las observaciones (así los signos negativos desaparecen), en obtener después su media aritmética y en extraer, finalmente, la raíz cuadrada de dicha media para volver a la unidad de medida original.
Otras medias estadísticas son la media aritmética, la media ponderada, media cuadrática, media generalizada, media armónica y la media aritmética geométrica.

MEDIA GEOMETRICA:
La media geométrica de una cantidad finita de números (digamos n números) es la raíz n-ésima del producto de todos los números.
Sólo es relevante la media geométrica si todos los números son positivos. Si uno de ellos es 0, entonces el resultado es 0. Si hay un número negativo (o una cantidad impar de ellos) entonces la media geométrica es, o bien negativa o bien inexistente en los números reales.
En muchas ocasiones se utiliza su trasformación en el manejo estadístico de variables con distribución no normal.
La media geométrica es relevante cuando varias cantidades son sumadas para producir un total.

¿COMENTARIO?

Las medidas de tendencia central le da significado a los datos de la frecuencia y representan los datos mas representativos que otros y siempre se encuentran en el medio de la grafica y se presentan por medio de formulas las cuales son LA MEDIA, LA MODA Y LA MEDIANA.

LA MEDIA: Es el promedio de la frecuencia o el numero de datos asignados.

LA MODA: Es el dato mas representativo de la frecuencia.

LA MEDIANA: Es el dato de la frecuencia que mas se repite.

LA DESVIACION ESTANDAR: Es la raiz cuadrada de los datos de la media aritmetica , la cual es transformar el dato negativo a positivo por medio de la elevacion al cuadrado y de la raiz para que el dato que de sea confiable.

LA DESVIACION MEDIA: Es la suma de todos los datos de la media aritmetica las cuales son divididas entre numerosn de la observacion.

LA MEDIA ARMONICA: Es es la que se representa por medio de una H la cual es una cantidad finita de numeros o la contraria de la media aritmetica y no se extiende anumeros nulos de la operacion.

LA MEDIA CUADRATICA: Esta es la suma de los datos de la raiz cuadrada dividido entre los numeros de la frecuencia.

LA MEDIA GEOMETRICA: Esta es cuando varias cantidads se suman para hacer un total ya que si la cantidad proporcionada hay un 0 el resultado siempre sera 0.

Estas formulas son utilizadas para llevar a cabo un presicion de datos de una frecuencia de n cantidad para poder formular de forma simultania y concreta.

SUMATORIA

La sumatoria es la parte de la estadistica que se ocupa de las suma de grandes cantidades de numeros determinados en la cual se utiliza el signo (SIGMA) que es una letra griega que significasuma ( Σ ) puedesumar cantidades infinitas. Son utilizadas para sumar numeros arbitrarios y naturales y se representa como N numeros. La sumatoria esta compuesta por:

( Σ ) : sigma letra griega que indica que debe realizarce la sumatoria

N: Es el limite superior de la sumatoria.

Xi: La variable con su indice representa el IESIMO elemento de conjunto.

i: Es el limite inderior de la sumatoria.

¡COMENTARIO?

En este tema creo que en la estadistica nos encontramos frecuentemente con la suma de gran número de terminos y para indicar que esos valores van a ser sumados se coloca el signo de suma que es ( Σ ) SIGMA la cual se puede combinar como las variables .

EL DIAGRAMA DE TALLOS Y HOJAS
Es una tecnica estadistica para representar un conjunto de datos. Cada valor numerico se divide en dos partes. EL o los digitos principales forman el tallo y los digitos secundarios las hojas. Los tallos estan colocados a lo largo de del eje vertical, y las hojas de cada observacion a lo largo del eje horizontal.

tallo hoja fa f f%

1 4,5,6,7,9 5 5 21.74

2 5,8,9 8 3 13.04

3 1,7 10 2 8.70

4 2,7,8 (3) 3 13.04

5 1,2,3,3,7 10 5 21.74

6 0,2,5,8 5 4 17.39

7 2 1 1 4.35

23// 100%//

?COMENTARIO?

En el diagrama de tallos y hojas se representa por numeros primarios que son los tallos asi como 15 y los secundarios son las hojas asi como 0 ose se representeria asi TALLOS=15-0=HOJAS esto se se multiplica y todos los datos se combierten a porcentajes y todos deben dar 100% para representa que la operacion es muy comprobable ejemplo:

en el ejercicio anterior F= a la frecuencia se toma el primer numero que en este caso es 5 y se divide por la cantidad de numeros que se tienen en este caso es 23 y se opera 5 /23 y se multiplica por 100 y asi se saca el porcentaje para realizar el diagrama de tallos y hojas.

DIAFRAMA DE CAJAS Y BIGOTES (BOX Y WHISKER PLOT)

Es la representacion visual que representa varias caracteristicas al mismo tiempo de un conjunto de datos importantes, tales como el centro, la dispersion, el alejamiento de la simetria, y la identificacion de valores extremos (puntos atipicos), es decir de, de valores que se alejen de una manera inusual de los demas datos. PResenta los tres cuartiles (y los valores minimos y maximos) alineados sobre una caja vertical u horizontal.

Para el diagrama de cajas y bigotes se requiere
Calcular la mediana y los otros dos cuartiles, con los cuales se formará la caja, que tiene la mediana como eje central, y como lados los dos cuartiles. Estos cuartiles reciben también los nombres de " bisagras".

La altura (anchura) de la caja no interesa.
La distancia H definida como la distancia entre el cuartil superior y el cuartil inferior, es decir, corresponde al rango intecuartílico

El paso correspondiente a 1.5 veces la distancia Þ Paso = 1.5 H
Cercas Internas, ubicadas a un paso de las bisagras o de los respectivos cuartiles, la cercainterna inferior menor que el valor mínimo de la muestra, ésta se hace igual al valor mínimo; igualmente, si la cerca interna superior da mayor que el valor máximo, ésta se hace igual a dicho valor.
Cercas Externas, ubicadas a un paso de las cercas internas. Así, las Cercas Externas Inferior (CEi) y Superior (CEs) estarán dadas.

COMENTARIO

En el diagrama de cajas y bigotes se calcula sacando la mediana y se puede colocar como sentro y los bigotes se representan como el dato mas pequeno hasta el mas grande y las cercas interiores s multiplican por 1.5(CIi+CIs) y las cercas extermas se multiplican por3(CEi+CEs) con esto podemos calcular una caja ya sea horizontal o vertical pero los datos deben guiarse por los cuartiles y la mediana para que el resultado sea positivo. Y esto se presentan por medio de formulas que se pueden cuantificar por medio de una frecuencia.

AREA BAJO LA CURVA NORMAL.

La altura maxima de la curva esta en la media, que en este caso es el promedio de todos los datos tabulados en una distribucion. Es asintoptica porque las colas de la curva no pueden tocar la línea de base. El rasgo más importante de la curva normal es susimetria, ya que si doblamos la curva en su punto mas alto creariamos dos mitades iguales, es unimodal porque solo tiene un punto máximo de frecunecia contiene el 100% de los datos a calcular.

COMENTARIO

en este tema el area bajocurva representa la altura maxima de la media y se puede hacer por medio de tabulacion de todos los datos de la frecuencia que se puede hacer porcentajey la pormula se calcula primero se toma el numero de frecuencias y se resta por la media y se divide por la desviacion estandart y se puede hacer tambien con la zona de normalidad y posee el 100% de datos a calcualr.